教科書の問題に出てくる数値は相当練られて作られています。小学校1年生の繰り上がりのたし算の問題は、ほとんどの教科書で「9+3」という数で問題が作られています。では、どうして9+3なのでしょうか。
9+2ではないの?
繰り上がりのたし算では10のまとまりを作ることが必須ですから、できるだけ10に近い数を用いた方がよいことになります。
1年生ではブロックを使って学習します。ブロック操作を少なくするという点からも10に近い数を用いることに異論はないでしょう。つまり、9を使用します。
また、たし算(加法)は、「たされる数+たす数」で表記されます。左の数が増えるイメージですから、左の数を10にしたいわけです。
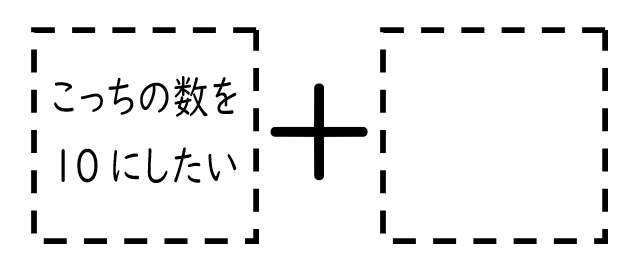
よって、「□+9」ではなく、「9+□」になります。
また、問題を作るとき、わかりやすさを考えると、できるだけ小さい数を用いた方がいいことは明らかです。
これらのことを踏まえると、繰り上がりのたし算で扱う問題は「9+2」となりそうですが、実は「9+2」という数を使用している教科書は皆無です。どうして「9+2」は除外されるのでしょうか。
9+2が除外される理由
繰り上がりのたし算で最も大切な考えは10のまとまりを作ることです。「9+2」という問題では、加数(たす数)である2を分解して10のまとまりを作ることになります。
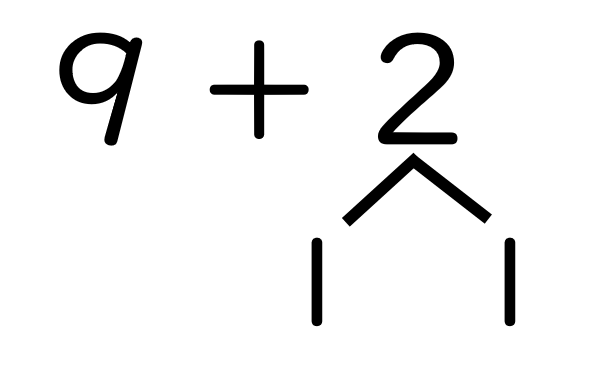
「9はあと1で10。2を1と1に分けて、9+1で10」
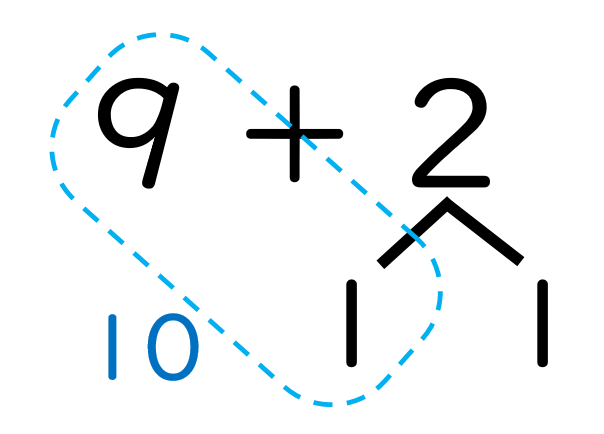
「10と1で11」と答えを出していきます。
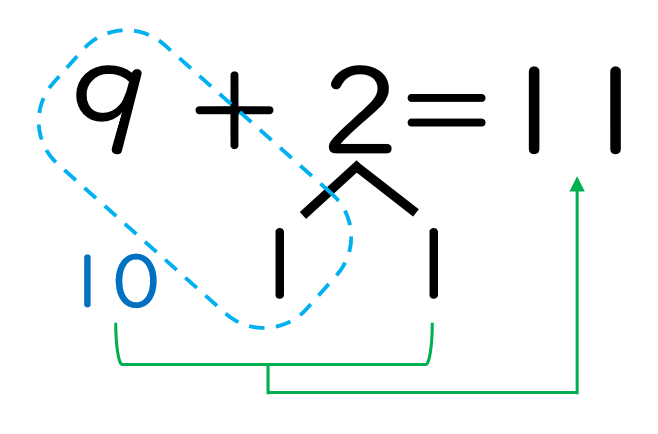
一見すると何も問題がないように見えますよね。しかし、実は小学校1年生はそんな単純ではありません。この学習で最も大切なポイントは10のまとまりを作るために2を1と1にわけるところです。しかし、2を分けるとなると分け方は1と1しかありませんし、2を単純に半分にしたと誤解してしまう児童が現れる可能性があります。
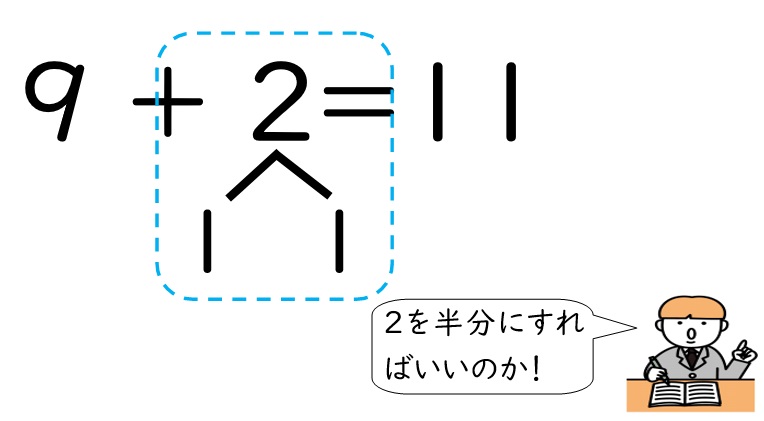
つまり、このような誤答が生じる可能性があるということです。
「まさか!そんなこと考えすぎだろ!」と思わる人もいるかもしれませんが、可能な限り、児童の躓きそうなポイントは排除するべきです。以上により、9+2は却下され、「9+3」という数を用いている教科書がほとんどなのです。
9+3でも不十分!?
「9+3」という数を用いている教科書がほとんどと言いましたが、実はたった1つの教科書だけ「9+3」を用いていません。「9+3」でも不十分であると考えられるのです。
児童の思考を深めたいなら、8+3!?
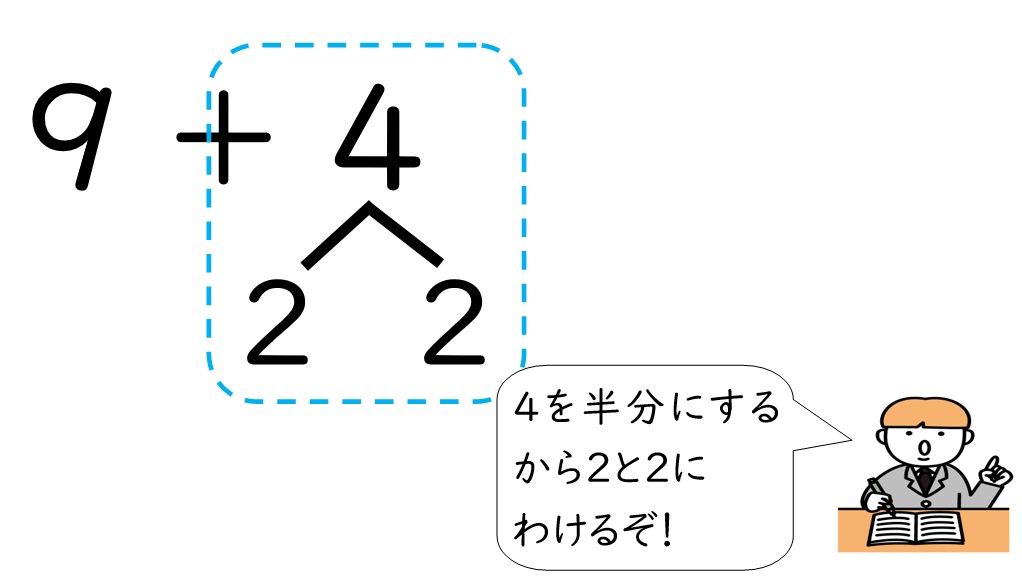
9+3にも、児童を脅かす穴があるのです。それは、3の分解と答えが混同されてしまうということです。3を1と2に分けますよね。この「1と2」と答えの「12」を混同してしまう可能性があるのです。
このように考えてしまった児童は次のような間違いをします。
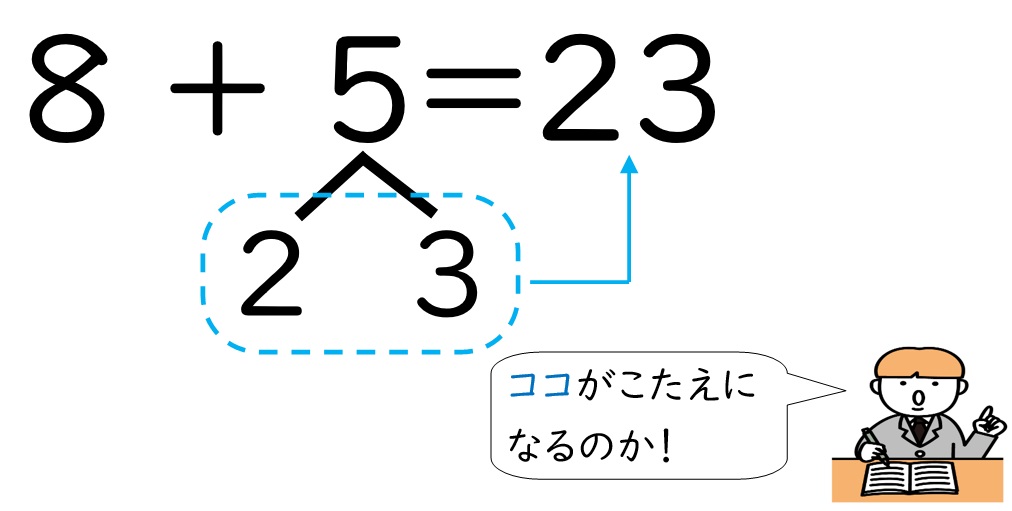
それでは「9+3」を用いていない教科書では、どの数値を扱っているのでしょうか。
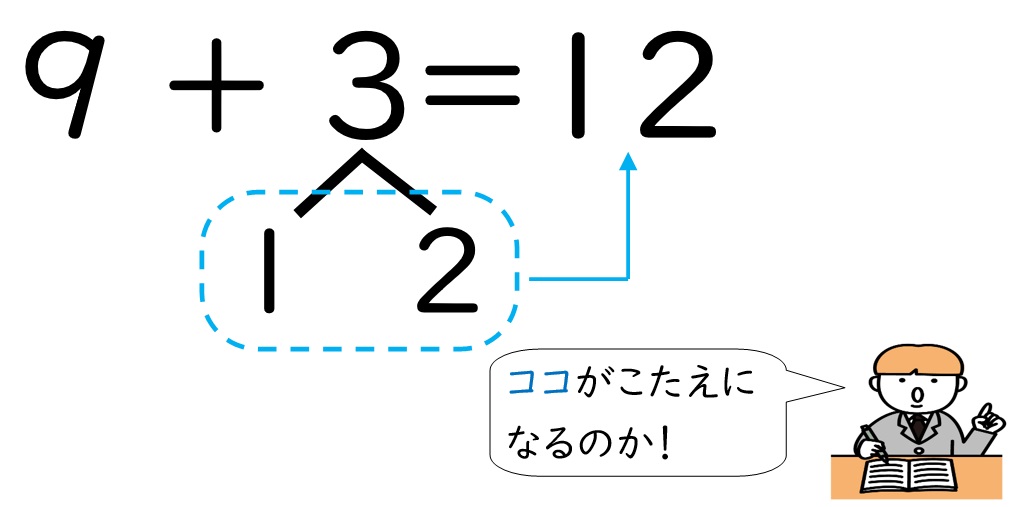
正解は「8+3」です!
8を10にするために、3を分解するのですが、3を1と2に分けるのではなく、3を2と1に分ける方が自然です。
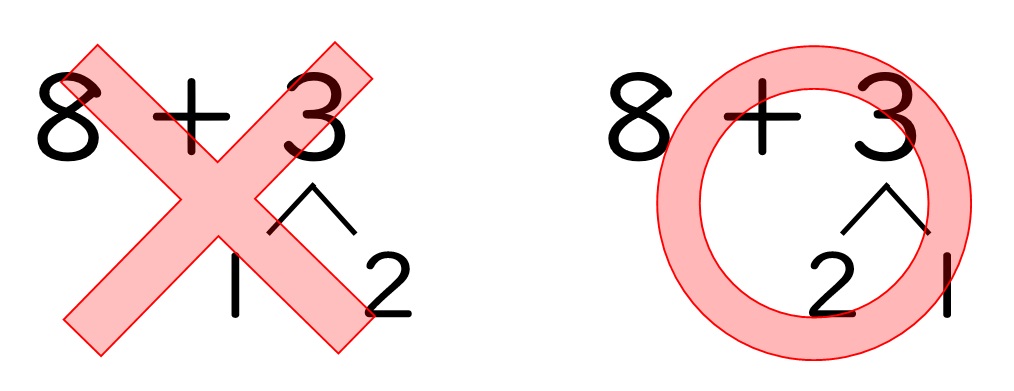
「10のまとまりを作りたい!」という本時のポイントをしっかりと意識させるためにも、
「8+3」という数値で問題を作っているのです。
問題を自作するときは要注意!
このように、教科書に出てくる問題の数値は吟味されて用いられています。研究授業などで問題を自作する教員も少なくないと思います。そのときには、扱う数値には相当気を遣う必要があるのです。
また、教材研究をする際には、「どうしてこの数値なのか。」「他の数値ではダメなのか。」という視点で問題を見つめると、新たな発見があることでしょう。


コメント